分布定数回路 P.112(2)

---

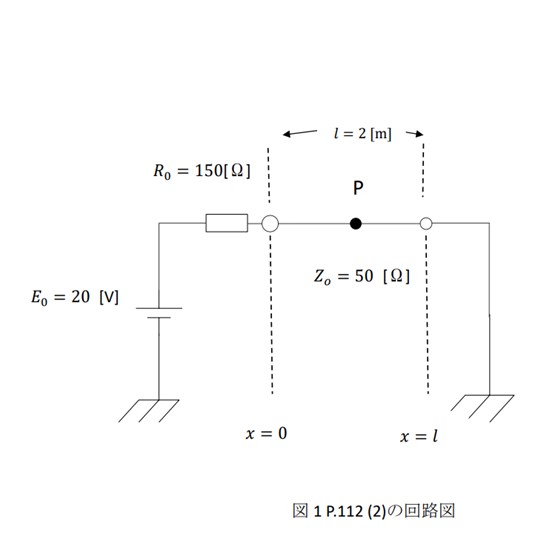
図1に示すように,
内部抵抗 \(R_{0} = 150 \) [Ω] , 起電力 \(E_{0} = 20 \) [V]
の直流電源を終端が短絡されている場合の無損失伝送線路
(特性インピーダンス \(Z_{0} = 50 \) [Ω] , 波の伝送速度 \(u_{p}\) = \(2\times10^8\) [m/s] , 長さ \({l} = 2 \) [m])
に接続した場合の線路中央の点Pの時間的な変化を求め, 図示せよ。

---

\({t} = 0 \) で \({x} = 0 \) の点 (送端) を出発する電圧波の大きさ\( E_{0}\) は, \[ E_0 = \frac{ZE}{Z+R} = \frac{50\times20}{50+150} = 5 [\mathrm{V}] \cdots(1) \] である。

電圧波が \({x} = 0 \)を出発して \({x} = {l}\) に到達するまでの伝搬時間 \({T}\) は, \[ T = \frac{l}{u_{p}} = \frac{2}{2 × 10^{8}} = 1 × 10^{-8} = 10 × 10^{-9} = 10 [\mathrm{ns}]\ \cdots(2) \] である。

伝送線路から負荷を見込んだ電圧反射係数 \(r_{v1}\)は, \[ r_{v1} = \frac{-Z_0}{Z_0} = \frac{-50}{50} = -1 \cdots(3) \] 電源内部を見込んだ電圧反射係数 \(r_{v2}\) は, \[ r_{v2} = \frac{R_0 - Z_0}{R_0 + Z_0} = \frac{150 - 50}{150 + 50} = \frac{100}{200} = 0.5 \cdots(4) \] である。

以上より, 最初の電源波が点 P に到達するまでの時間は \(5\) ns
→ \({t} = 0 ～ 5\) ns : \(0\) V \(\cdots(5)\)

点 P に到達, 点 P は \(5\) V の電圧がかかる
→ \({t} = 5\) ns : \(5\) V \(\cdots(6)\)

電圧は 5V のまま終端 \({x} = {l} \) へ到達, \({x} = {l} \) では電圧反発係数 \(r_{v1}\) は \(-1\) なので, \(5\) V の電圧が \(-5\) V の電圧となって電源端 \({x} = 0 \) に進む。
→ \({t} = 5 ～ 15\) ns : \(5\) V \(\cdots(7)\)

点 P に到達, このとき電圧は打ち消しあって点 P は \(0\) V となる
→ \({t} = 15\) ns : \(0\) V \(\cdots(8)\)

電圧は \(-5\) V のまま電源端 \({x} = 0 \) へ到達, \({x} = 0 \) では電圧反射係数 \(r_{v2}\)が \(0.5\) なので、\(-5\) V の電圧が \(-2.5\) V の電圧となって終端 \({x} = {l} \) に再度進む
→ \({t} = 15 ～ 25\) ns : \(0\) V \(\cdots(9)\)

点 P に到達, 点 P は \(-2.5\) V の電圧がかかる
→ \({t} = 25\) ns : \(-2.5\) V \(\cdots(10)\)

その後, 終端にて \(-1\) で反射, 電源端にて \(0.5\) で反射を繰り返し, \(t \to \infty\)では電圧は 0 となる。
(5)～(10)までの条件を基にして描いた波形を 図2 に示します。
また, 終端にて \(-1\) で反射されて電圧が 0 になっている様子を表した波形を 図3 に示します。
以上より, 直流電源を終端が短絡されている場合の無損失伝送線路に接続した場合の
線路中央の点Pの時間的な変化を表した図は 図4 となります。
理解を助けるために, 図4 を動かしたものを 図5 となります。