アンペールの法則

アンペールの実験
エルステッドによる電流と磁界の関係の発見後、アンペールは様々な実験を行いこれを定量化した。
先に紹介した右ねじの法則もこのアンペールの法則に含まれる。

Chapter01 ～平行に並んだ電線間働く力の発見～

---

アンペールは平行に並んだ導線間に働く力を実験により発見した。
図は平行な2本の無限長導体の3次元イメージである。
この時、導線に流れる電流をそれぞれI₁、I₂、線間距離をrとした時の線間に発生する力Fは

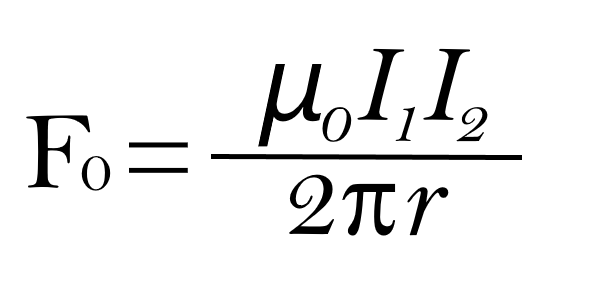
となる。μ₀は真空での透磁率を示す。
次になぜ、この式が成り立つかを次に解説する。

まず、電流の関係について下図に示す。

図にあるように、電流の向きにより力の向きが変化し、電流の大きさに対して力の大きさは比例関係である。力の方向は電流I₁、I₂の正負に依存する。

次に線間距離の関係について同じように解説する。

図のように線間の距離が近づくほど力がより強くなり、離れるほど弱くなる。すなわち反比例の関係となっている為、距離rは式では分母に来る


次に透磁率μ₀だが、「電流の話なのになぜ磁界の強さと磁束密度の比例係数を示す透磁率が出るのさ」と感じた君は鋭い。
ここで、アンペールの法則の説明の前に学習したことを思い出してみよう。

電流が発生する時磁界も右ねじの法則により同時に発生すると説明をした。



そう、ここで考えている平行導線にも同じように磁界が発生するのだ。


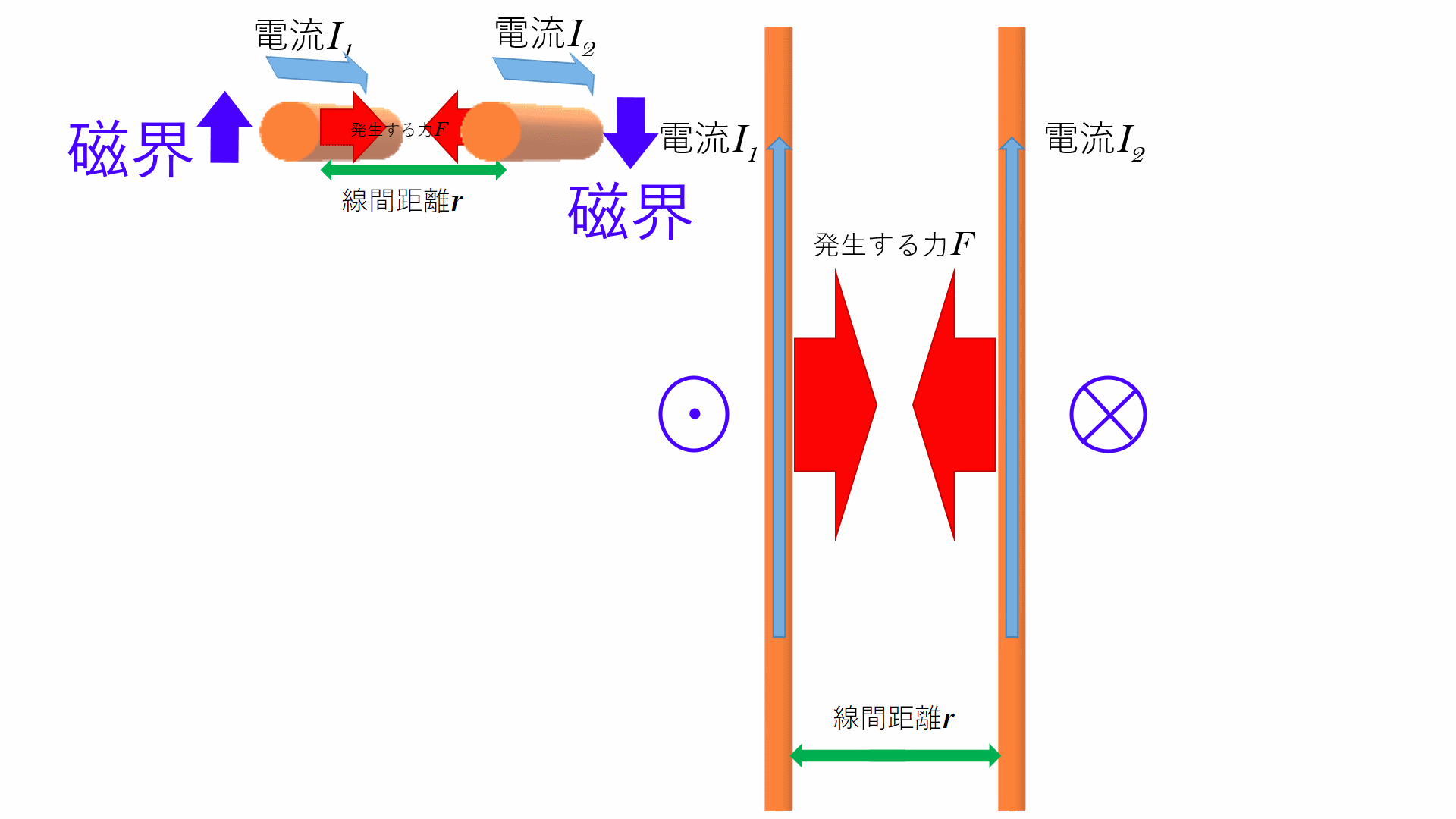
図のように磁界が生じる。これが透磁率μ₀が関係してくる理由である。
また、この時の電流、磁界、力がそれぞれ垂直に発生する。この関係から生まれたのがジョン・フレミングが発表した後のフレミング左手の法則である。

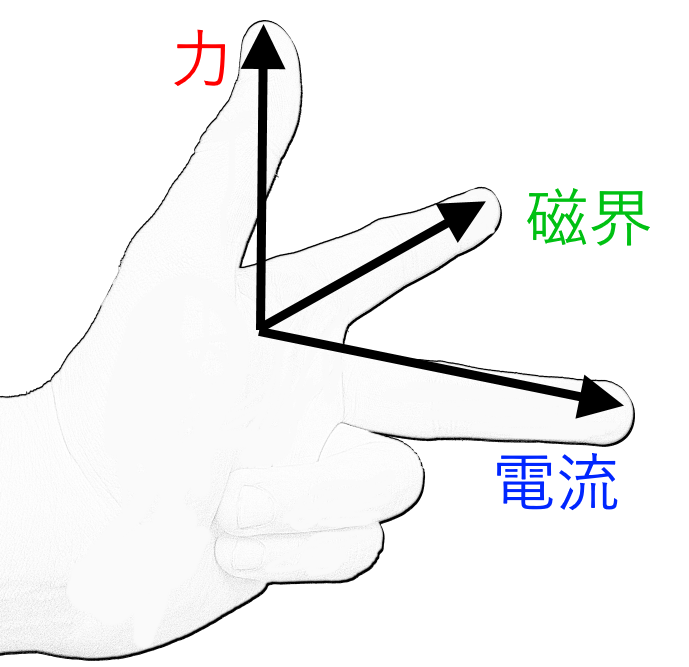
以上の関係により平行導線間のちからの関係が成り立つのである。
また、ここで登場したフレミングの法則がモーター(電動機)において基礎になる法則である。