電界

Chapter4 ～電位と電位差～

電位

　上図に示すように、一様な電界\(\boldsymbol{E}\)[N/C]の中に置かれた点電荷\(q\)[C]は、電気力\(\boldsymbol{V}=q\boldsymbol{E}\)[N]を受ける。したがって、電荷が電界の向きに距離\(d\)[m]移動するとき、電界のする仕事\(W\)[J]は
\[W =Fd=qEd=qV\]
と表される。ここで電位差\(V\)(電圧)と電界\(E\)は
\[V =Ed\] または \[E= \frac{V}{d}\] の関係がある。電位差の単位はV(ボルト)である。電界の単位は[V/m]で表される。

等電位線

　電位とは、地図でいうと山の高さに相当する。山が高いほど（電位が高いほど）エネルギーは大きい。ではこの勾配は何を表すか。
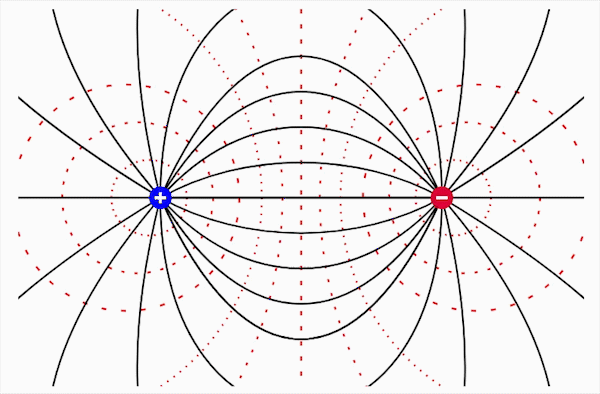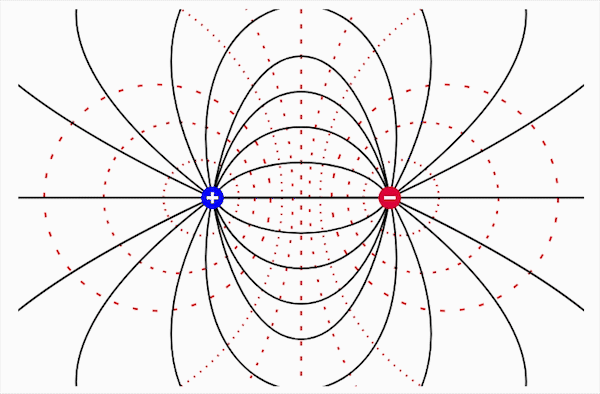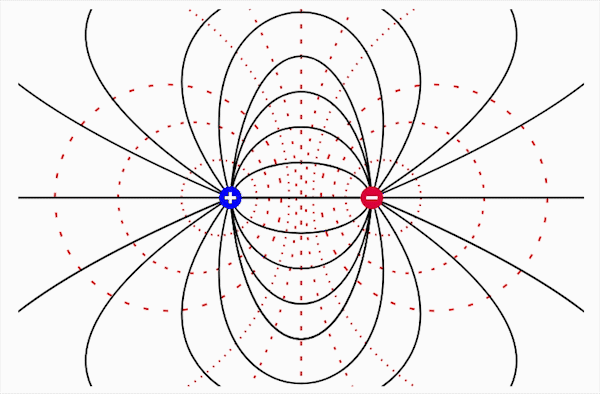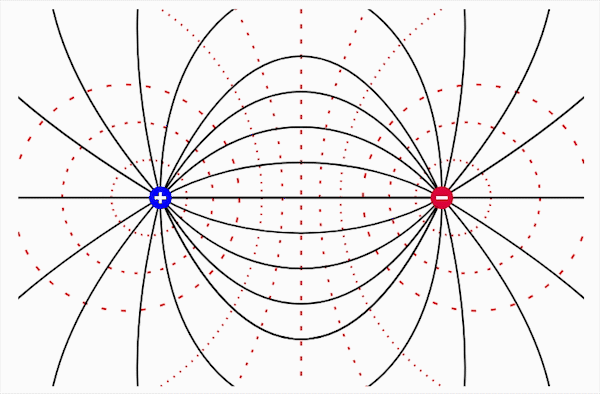
静電界は静止した電荷を源泉とするベクトル場である。このベクトル場からスカラー量である電位が定義された。このように、空間の各点でスカラー量が定義される場をスカラー場という。電位の場はスカラー場である。
　電位Ｖのスカラー場が与えられたとき電界\(\boldsymbol{E}\)を導くにはどう考えるか。
　接近した2点\(P_1\),\(P_2\)をとる。\(P_1\)での電界を\(\boldsymbol{E}\)、両点を結ぶ微小ベクトルを\(d\boldsymbol{s}\)とする。このとき、 \[V_{12}=V_{P_2}-V_{P_1} = \frac {W_{12}} {q} \] \[=-\int_{P_{1}}^{P_{2}} \boldsymbol{E}・d \boldsymbol{s} \] であるから、\(d\boldsymbol{s}\)が十分小さいとすれば、微小電位差\(dV\)は \[dV=-\boldsymbol{E・}d\boldsymbol{s}\] \[=-E・\mathrm{cos}\theta・ds=-E_sds \] ここで、\(\theta\)は\(\boldsymbol{E}\)と\(d\boldsymbol{s}\)のなす角度であり、\(E_s\)は点\(P_1\)における電界\(\boldsymbol{E}\)のs方向成分、すなわち、\(E_s \mathrm{cos}\theta\)である。したがって \[E_s=-\frac{dV}{ds}\] が導かれる。このようにして、任意の方向の電界の成分を求めることが出来る。直交座標の場合に、\(x,y,z\)方向の成分は \[E_x=-\frac{\partial V}{\partial x},\] \[E_y=-\frac{\partial V}{\partial y},\] \[E_z=-\frac{\partial V}{\partial z}\] によって与えられる。このように電界ベクトル\(\boldsymbol{E}\)の\(x,y,z\)成分を電位\(V\)で示せるから、\(\boldsymbol{E}\)の表式としては \[E=E_x\boldsymbol{i}+E_y\boldsymbol{j}+E_z\boldsymbol{k}\] \[=-(\boldsymbol{i}\frac{\partial V}{\partial x}+\boldsymbol{j}\frac{\partial V}{\partial y}+\boldsymbol{k}\frac{\partial V}{\partial z})\] これをgrad\(V\)で表すと \[\mathrm{grad} V=∇V\] \[=\boldsymbol{i}\frac{\partial V}{\partial x}+\boldsymbol{j}\frac{\partial V}{\partial y}+\boldsymbol{k}\frac{\partial V}{\partial z}\] これを簡潔に書くと \[\boldsymbol{E}=-\mathrm{grad}V=-∇V\] これが\(V\)から電界\(\boldsymbol{E}\)を導くことが出来る。　電位の等しい点を連ねてできる面を等電位面という。上図に正負等量の電荷の作る電界と等電位面の様子を示す。
一定の電位差ごとに等電位面をかくと、間隔が狭いところほど電界が強い。一般に等電位面は電気力線に垂直である。（図はイメージです）
等電位線は地図でいう等高線に相当する。

地図でいうと正電荷は山、負電荷は谷と置き換えて考えるとイメージできるだろうか。
ただし、この電荷の現象は平面上での現象である、ここでは電位差を高低差と例えている。

～電位と電位差～
Chapter3～電気力線と電束～

項目一覧へ