コンデンサの電気量と静電容量
電気量とは、電荷の量を示す。
静電容量とは、コンデンサにどのくらい電荷を蓄えられるかを示す。
静電容量の利用例
電気量の式
コンデンサに蓄えることができる容量のことを電気量という。
電気量はQで表され単位は[C]クーロンである。
コンデンサにおける電気量の関係は
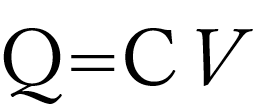
となる。
この時のVは電極間の電位差を表し、Cは静電容量を表す。
このとき静電容量Cは比例係数であり、電気量Qは電位差VのCの定数倍であることを示している。
この関係はどのような形の導体間にも必ず成り立つ。
1.任意の形をした導体間の静電容量
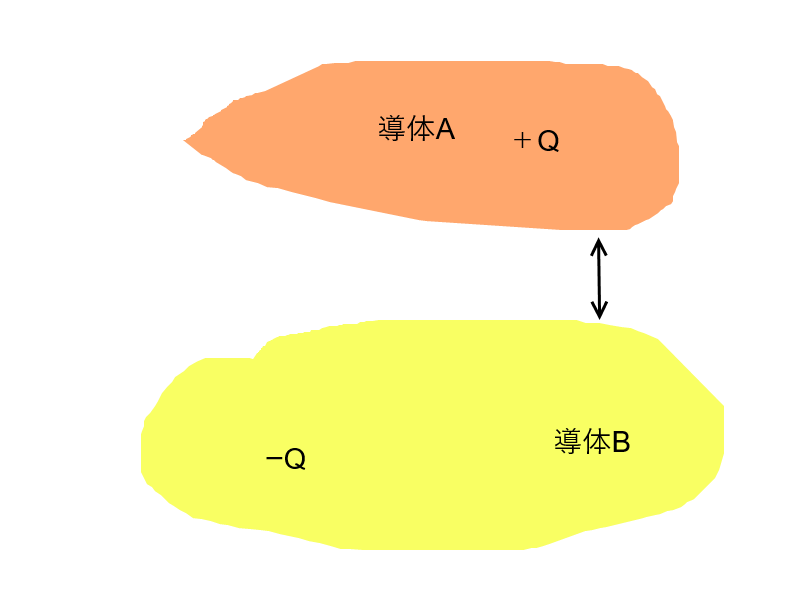
この時静電容量は
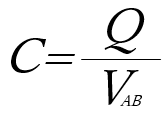
から求めることができる。
導体とは、どの点においても電位は同じであるため、図のような導体AB間の電位差は一定となる。
この時静電容量は上の式より
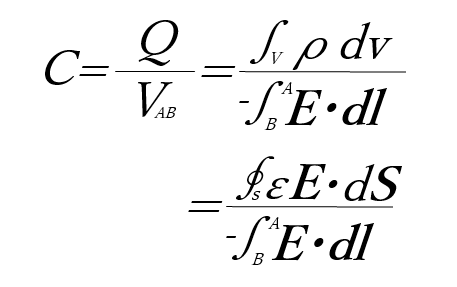
となる。
Eは電界、εは誘電率を表す。
また最後の式の分子は面積の積分(面積分)であるから、静電容量は誘電率と導体の形状によって決まることを示している。
任意導体AB間の電位差VABは
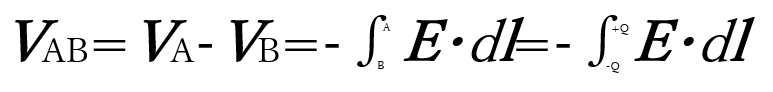
となる。
これは距離が有限である場合であり、導体Aと導体Bの間が離れすぎる状態(無限遠)となった場合、導体Bの電位VBは、
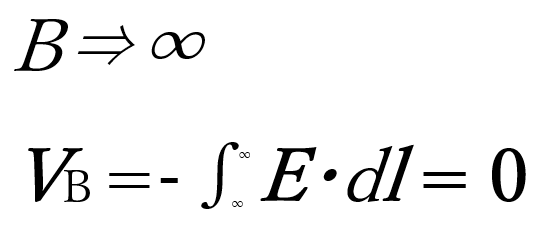
となる。
この式を電位差VABの式に代入すると
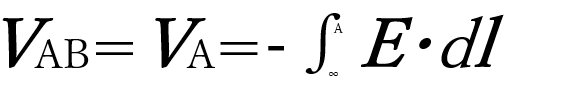
となる。
導体Bの距離が離れすぎると導体Aの電位のみが出てくる。
すなわち、この場合の電気容量は、
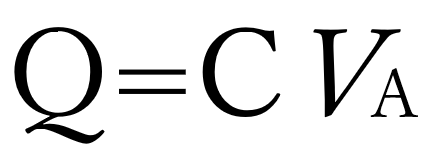
となる。また静電容量は、
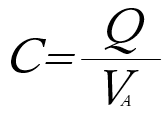
となる。
2.単球導体の静電容量
次に、単球導体を対象に考えてみる。
下図に単体の導体球を示す。

半径をa、導体が持つ電荷Qのとき電位Vは
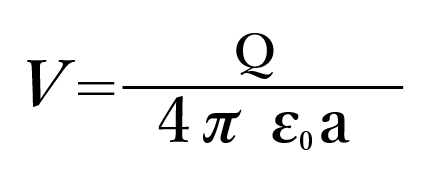
となる。
これは半径aの球の中心から距離aの位置、つまり球の表面上の電位を示す。
この時の静電容量は、
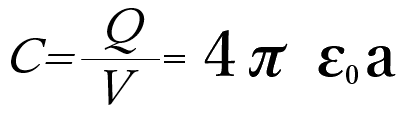
となる。
2.同心球
同心球とは、同じ点を中心とした球体であり下図はその断面図である。

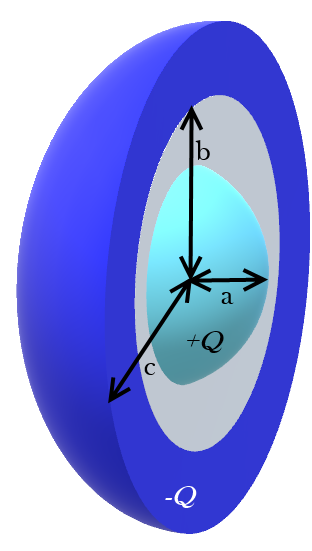
この断面図見覚えがあると思った人もいるであろう。
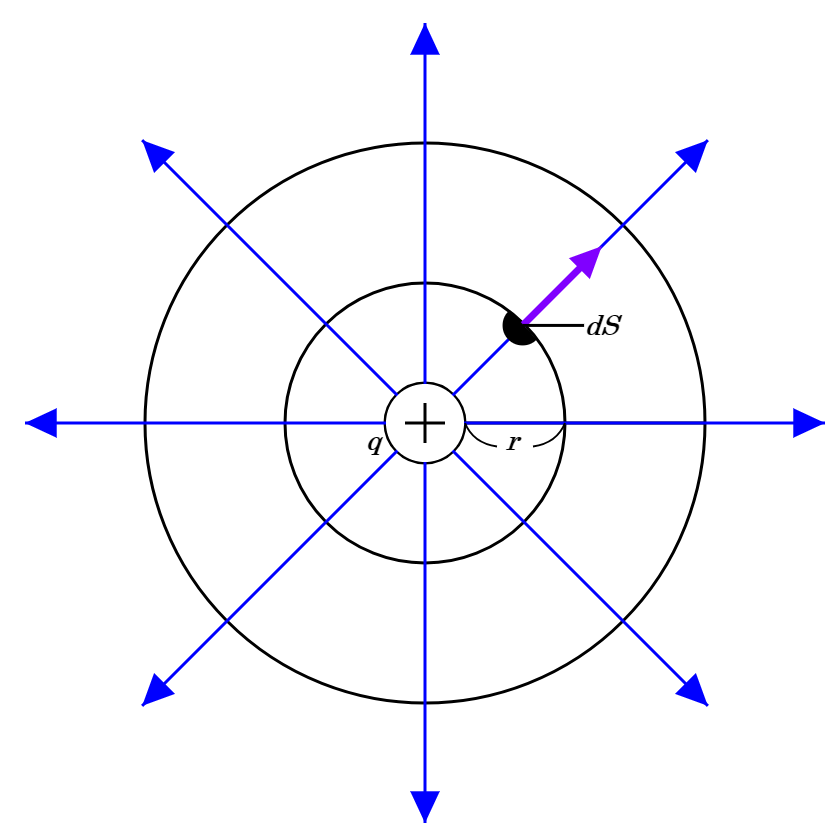
この図は中心の正電荷から出る電気力線を示している。
電気力線とは、電界の方向と電界の密度が電界の強さを示す。
電界と電気力線の関係をガウスの法則から求められるので、
この時の点rにおける(a<r<b)電界は
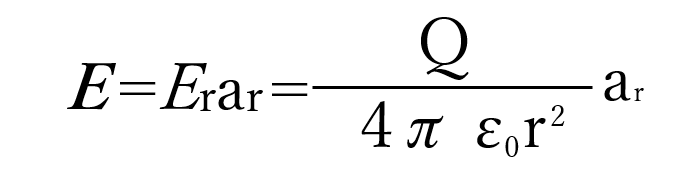
となる。
なお、この時の電界はベクトル成分であるため式の中でスカラー量に変換している。
そのためarは方向成分を示している。
電位差は
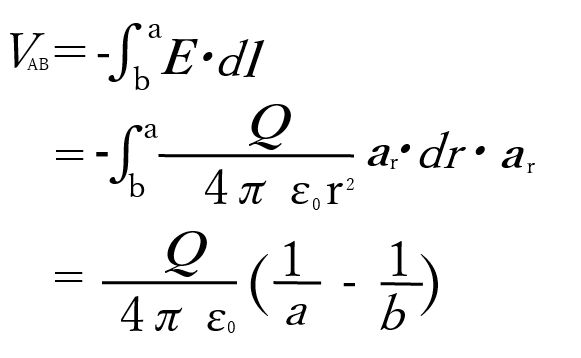
となる。
静電容量は、
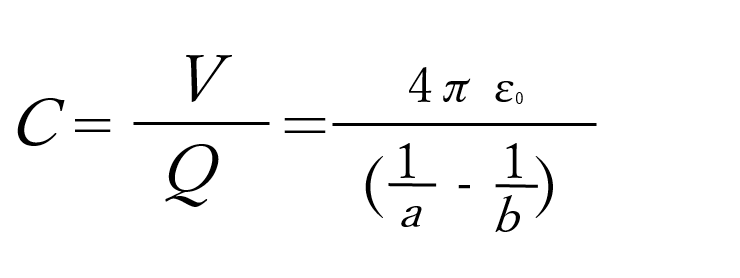
となる。
この時、内側の球aと外側の球b間の距離が無限遠となった場合、
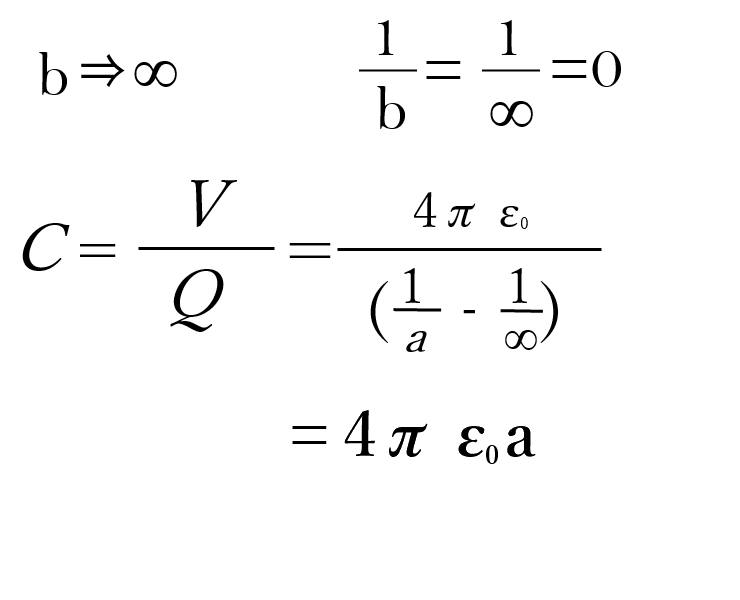
となる。
これは、単心球と同じ結果となる。
3.平行平板 平行平板コンデンサとは、文字通り平板電極が平行に並んだコンデンサである。


図のように、面積\(S\)の平行に並んだ電極を考える。
この電極にそれぞれ\(+Q\)、\(-Q\)の電荷を与えると電荷の密度は
\(+\sigma=\frac{+Q}{S}\) 、 \(-\sigma=\frac{- Q}{S}\)
となる。この時の電界の強さは、
\(E=\frac{\sigma}{\varepsilon_0}\)
となり、平行に向き合う電極間の電位差は、平板間距離\(d\)を用いて、
\(V=Ed=\frac{\sigma}{\varepsilon_0 d}=\frac{Q}{\varepsilon_0 S }d\)
となる。
コンデンサの基本式を用いて、平行平板コンデンサの電気容量を表すと、 \[C = \frac{Q}{V}=\frac{\varepsilon_0 S}{d}\] となる。
式からわかるように、平行平板コンデンサは他のコンデンサとくらべて式がシンプルであり、真空の比誘電率\(\varepsilon_0\)、平行板面積\(S\)、平行板距離\(d\)が求められれば、簡単に定量化できる。
このため多くの教材でコンデンサの例として用いられる。
ここで注意してほしいが、簡単であるため説明に平行平板コンデンサを用いるが、これまで説明してきたとおりこれはあくまで一例であり、全てに適応できるものではない。
改めて、電気容量は、
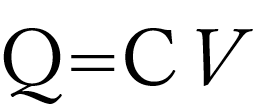
この式で表されることを覚えておいてほしい。
~コーヒーブレイク~
平行平板間に電界を発生できるのか、実際にやってみた。
このように、電極間に電圧を印加することで電界が発生することがおわかりいただけるだろうか。
コンデンサは電圧を貯めたり、出したりすることで電圧の安定化やノイズ除去などができる。
ホームに戻る
静電容量とは、コンデンサにどのくらい電荷を蓄えられるかを示す。
静電容量の利用例
コンデンサに蓄えることができる容量のことを電気量という。
電気量はQで表され単位は[C]クーロンである。
コンデンサにおける電気量の関係は
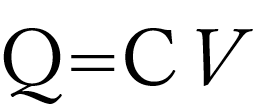
となる。
この時のVは電極間の電位差を表し、Cは静電容量を表す。
このとき静電容量Cは比例係数であり、電気量Qは電位差VのCの定数倍であることを示している。
この関係はどのような形の導体間にも必ず成り立つ。
1.任意の形をした導体間の静電容量

この時静電容量は
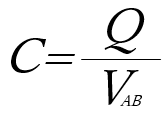
から求めることができる。
導体とは、どの点においても電位は同じであるため、図のような導体AB間の電位差は一定となる。
この時静電容量は上の式より
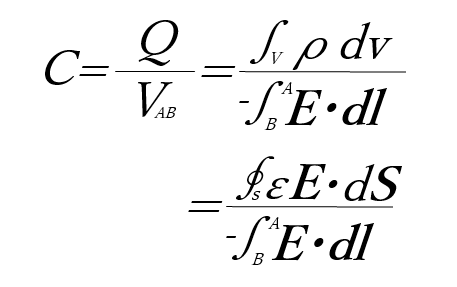
となる。
Eは電界、εは誘電率を表す。
また最後の式の分子は面積の積分(面積分)であるから、静電容量は誘電率と導体の形状によって決まることを示している。
任意導体AB間の電位差VABは
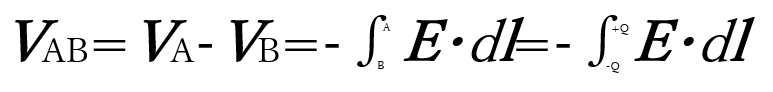
となる。
これは距離が有限である場合であり、導体Aと導体Bの間が離れすぎる状態(無限遠)となった場合、導体Bの電位VBは、
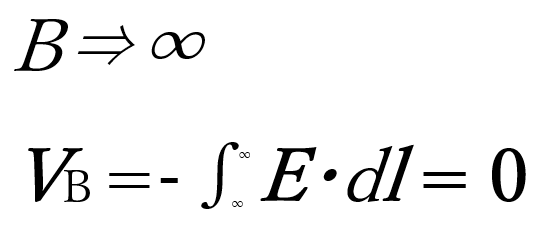
となる。
この式を電位差VABの式に代入すると
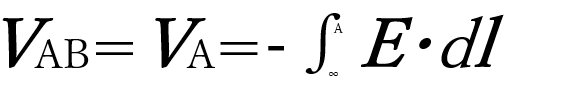
となる。
導体Bの距離が離れすぎると導体Aの電位のみが出てくる。
すなわち、この場合の電気容量は、
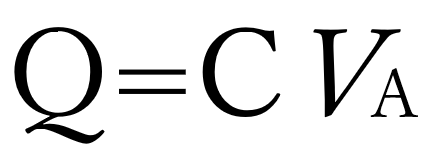
となる。また静電容量は、
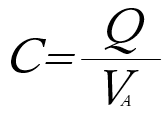
となる。
2.単球導体の静電容量
次に、単球導体を対象に考えてみる。
下図に単体の導体球を示す。

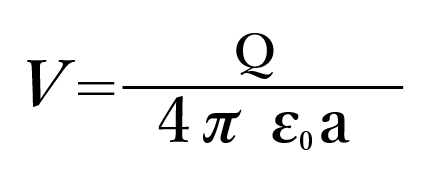
となる。
これは半径aの球の中心から距離aの位置、つまり球の表面上の電位を示す。
この時の静電容量は、
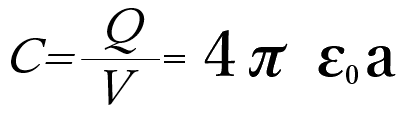
となる。
2.同心球
同心球とは、同じ点を中心とした球体であり下図はその断面図である。



この図は中心の正電荷から出る電気力線を示している。
電気力線とは、電界の方向と電界の密度が電界の強さを示す。
電界と電気力線の関係をガウスの法則から求められるので、
この時の点rにおける(a<r<b)電界は
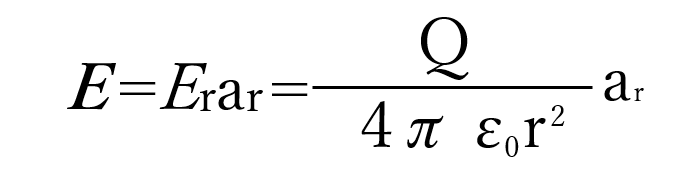
となる。
なお、この時の電界はベクトル成分であるため式の中でスカラー量に変換している。
そのためarは方向成分を示している。
電位差は
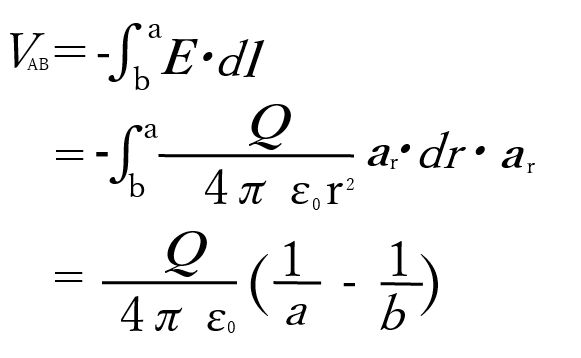
となる。
静電容量は、
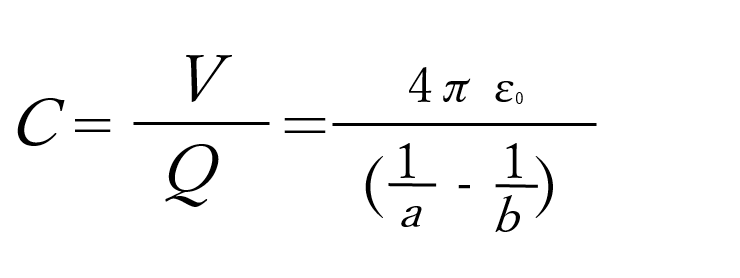
となる。
この時、内側の球aと外側の球b間の距離が無限遠となった場合、
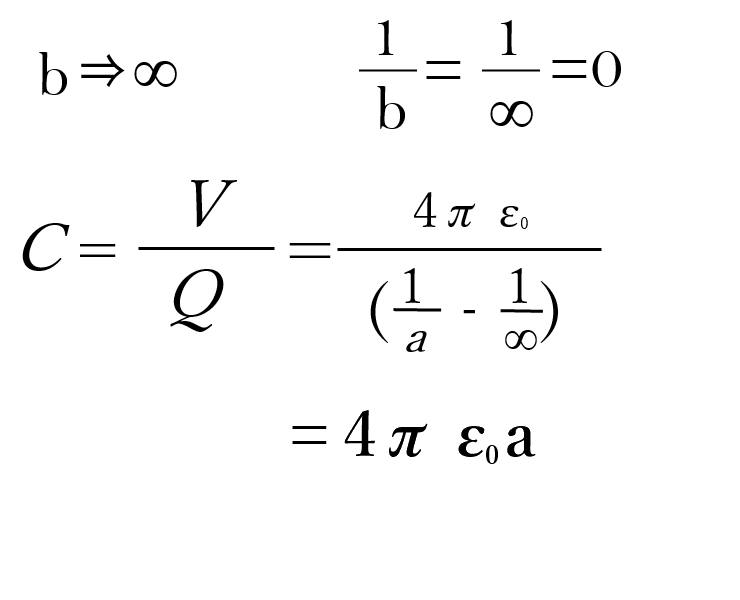
となる。
これは、単心球と同じ結果となる。
3.平行平板 平行平板コンデンサとは、文字通り平板電極が平行に並んだコンデンサである。


図のように、面積\(S\)の平行に並んだ電極を考える。
この電極にそれぞれ\(+Q\)、\(-Q\)の電荷を与えると電荷の密度は
\(+\sigma=\frac{+Q}{S}\) 、 \(-\sigma=\frac{- Q}{S}\)
となる。この時の電界の強さは、
\(E=\frac{\sigma}{\varepsilon_0}\)
となり、平行に向き合う電極間の電位差は、平板間距離\(d\)を用いて、
\(V=Ed=\frac{\sigma}{\varepsilon_0 d}=\frac{Q}{\varepsilon_0 S }d\)
となる。
コンデンサの基本式を用いて、平行平板コンデンサの電気容量を表すと、 \[C = \frac{Q}{V}=\frac{\varepsilon_0 S}{d}\] となる。
式からわかるように、平行平板コンデンサは他のコンデンサとくらべて式がシンプルであり、真空の比誘電率\(\varepsilon_0\)、平行板面積\(S\)、平行板距離\(d\)が求められれば、簡単に定量化できる。
このため多くの教材でコンデンサの例として用いられる。
改めて、電気容量は、
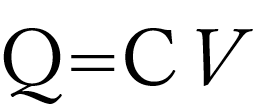
この式で表されることを覚えておいてほしい。
平行平板間に電界を発生できるのか、実際にやってみた。
コンデンサは電圧を貯めたり、出したりすることで電圧の安定化やノイズ除去などができる。
ホームに戻る