ガウスの法則
ガウスの法則が表すもの
電束についての性質が成立するならば、電気力線に関する次の性質が成り立つ。
閉じた面を貫いて外へ出ていく電気力線の総本数は、その面に包まれた中の電荷に比例する。
よくこう言われているが、電気力線は面を垂直に貫く性質がある。また、電気力線は必ず電荷から発生する。
この2つから、上記の下線を引いた一文が成り立つ。
これがガウスの法則の直感的な表現である。
早速ガウスの法則の証明に入っていく。
いま、原点のある点電荷\(q\)の周りに半径\(r\)の球面を考える。実際には任意の図形で構わないが、ここでは簡単のため球を考える。
この球面を通過する電気力線の総本数\(Φ_e\)は、
\[Φ_e=\int_S \boldsymbol{E・n}dS=\int_SE_ndS\]
と表す。このとき電界\(E_n\)は
\[E_n=\frac{q}{4\piε_0r^2}\] であり、また、\(dS\)は面積であるから、 \[Φ_e=\int_{S_0}\frac{q}{4\piε_0r^2}dS=\frac{q}{4\piε_0r^2}・{4\pi r^2}\] \[=\frac{q}{ε_0}\] この値は明らかに、\(r\)の値には無関係、すなわち、任意の大きさの球面で成り立つことがわかる。
任意に考えた二つの球面ではさまれた場所では電気力線は発生も消滅もしないということになる。
ここで、上の図に示すように、任意の二つの大小球面を考える。\(r\)の値には無関係であるから、小球面を出る電気力線の数と大球面を出る電気力線の数は等しい。したがって、法則が成り立つ。
閉曲面を貫いて外へ出ていく電気力線の総本数は、この面に包み込まれている電荷に比例する。
\[Φ_e=\int_{S_0} {E・n}dS=\frac{q}{ε_0}\]
この法則をガウスの法則といい、電界の空間分布と電荷を結びつける。
さらに、電気力線の性質
「電気力線は閉曲線にはならない」
から
という法則によって、電荷分布から電界を一意的に決定できる。
また、その電界はクーロンの法則から求めたものと一致する。
次に、点電荷の集まりが作る電界は、各電荷がつくる電界\(E_i\)の和である。すなわち、重ね合わせの原理に従って考えればよく、ある閉曲面\(S_0\)について、内部に \(q_i\)が\(n\)個あれば、
\[Φ_e=\int_{S_0} {E・n}dS=\frac{1}{ε_0}\sum_{i=1}^{n}q_i\]
さらに、閉曲面\(S_0\)の中で電荷が密度\(ρ\)で分布しているならば、その中に含まれる電荷の総量は\(ρ\)の体積積分で与えられるから
\[Φ_e=\int_{S_0} {E・n}dS=\frac{1}{ε_0}\int_{V}ρdV\] このようになる。
このガウスの法則は、積分形のガウスの法則とも呼ばれてる。また、ガウスの定理と呼ばれている数学の公式を使うことによって、この法則を微分の形で表すことが出来る。 しかし、積分形では、ある程度広がった範囲の電界をまとめて扱うという場合でしか使えない。微分系では広がった範囲の電界ではなく、空間上のある一点の電界を扱うイメージ。
数学におけるガウスの定理は、またの名をベクトルの発散という。
\[\int \boldsymbol{E・n}dS=\int {\mathrm{div}\boldsymbol{E}}dV\] という式で表される。右辺に含まれる\(\mathrm{div}\boldsymbol{E}\)というのは単位体積当たりから湧き出してくる電場の大きさ(発散)を表している。 各方向の変化を足したものと考えてよい。
\[\mathrm{div}\boldsymbol{E}=\nabla・\boldsymbol{E}=\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\] と定義できる。
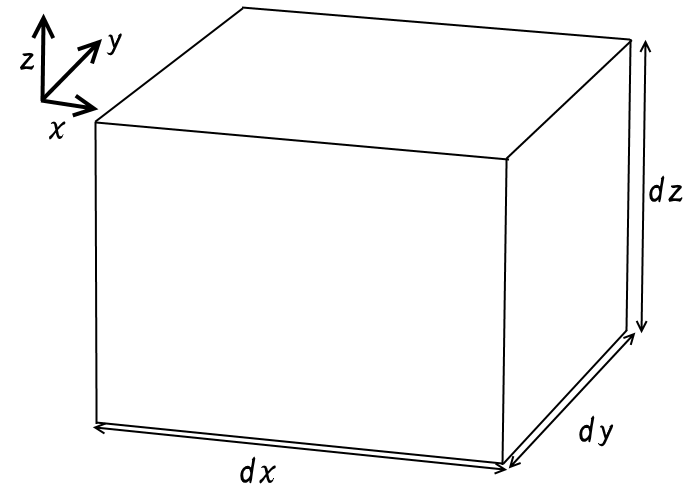
下図に示すように、Pを一つの頂点として、各座標軸にそって立方体を考えよう。この六つの面を通って出ていく電気力線の総本数が直方体の内部の電荷と関係付けられている。 まずx軸に垂直な二つの面、図では右と左の面、を考える。外向きの法線方向は、右側ではx、左面では-x方向である。面内での\(E_x\)の変化を無視すれば、積分のこの部分は、
\[E_x(x + \Delta x,y,z)\Delta y\Delta z-E_x(x ,y,z)\Delta y\Delta z\] \[\simeq \frac{ \partial E_x }{ \partial x }\Delta x\Delta y\Delta z\] と近似できる。同様にy軸、z軸に垂直な2くみの面の寄与を求めこれらを足して電気力線の合計を出すと
\[\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\Delta x\Delta y\Delta z\]
一方、直方体の中にある電荷は、体積密度を\(\rho\)とすれば\(\rho\Delta x\Delta y\Delta z\)と近似できる。これらを先の積分式に入れると、ガウスの法則は、
\[\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\Delta x\Delta y\Delta z=\frac{\rho}{\epsilon_0}\Delta x\Delta y\Delta z\] と書くことが出来る。
この式から\(\Delta x\Delta y\Delta z\)を消去し、ナブラで表現すれば
\[\mathrm{div}\boldsymbol{E}=\nabla・\boldsymbol{E}=\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }=\frac{\rho}{\epsilon_0}\]
と表すことが出来る。
ガウスの法則は磁界の磁束に対しても適応できる。この説明は別途説明する。
電気力線と電束
磁束線
ホームに戻る
閉じた面を貫いて外へ出ていく電気力線の総本数は、その面に包まれた中の電荷に比例する。
よくこう言われているが、電気力線は面を垂直に貫く性質がある。また、電気力線は必ず電荷から発生する。
この2つから、上記の下線を引いた一文が成り立つ。
これがガウスの法則の直感的な表現である。
早速ガウスの法則の証明に入っていく。
いま、原点のある点電荷\(q\)の周りに半径\(r\)の球面を考える。実際には任意の図形で構わないが、ここでは簡単のため球を考える。
\[E_n=\frac{q}{4\piε_0r^2}\] であり、また、\(dS\)は面積であるから、 \[Φ_e=\int_{S_0}\frac{q}{4\piε_0r^2}dS=\frac{q}{4\piε_0r^2}・{4\pi r^2}\] \[=\frac{q}{ε_0}\] この値は明らかに、\(r\)の値には無関係、すなわち、任意の大きさの球面で成り立つことがわかる。
任意に考えた二つの球面ではさまれた場所では電気力線は発生も消滅もしないということになる。
ここで、上の図に示すように、任意の二つの大小球面を考える。\(r\)の値には無関係であるから、小球面を出る電気力線の数と大球面を出る電気力線の数は等しい。したがって、法則が成り立つ。
閉曲面を貫いて外へ出ていく電気力線の総本数は、この面に包み込まれている電荷に比例する。
\[Φ_e=\int_{S_0} {E・n}dS=\frac{q}{ε_0}\]
この法則をガウスの法則といい、電界の空間分布と電荷を結びつける。
さらに、電気力線の性質
という法則によって、電荷分布から電界を一意的に決定できる。
また、その電界はクーロンの法則から求めたものと一致する。
次に、点電荷の集まりが作る電界は、各電荷がつくる電界\(E_i\)の和である。すなわち、重ね合わせの原理に従って考えればよく、ある閉曲面\(S_0\)について、内部に \(q_i\)が\(n\)個あれば、
\[Φ_e=\int_{S_0} {E・n}dS=\frac{1}{ε_0}\sum_{i=1}^{n}q_i\]
さらに、閉曲面\(S_0\)の中で電荷が密度\(ρ\)で分布しているならば、その中に含まれる電荷の総量は\(ρ\)の体積積分で与えられるから
\[Φ_e=\int_{S_0} {E・n}dS=\frac{1}{ε_0}\int_{V}ρdV\] このようになる。
このガウスの法則は、積分形のガウスの法則とも呼ばれてる。また、ガウスの定理と呼ばれている数学の公式を使うことによって、この法則を微分の形で表すことが出来る。 しかし、積分形では、ある程度広がった範囲の電界をまとめて扱うという場合でしか使えない。微分系では広がった範囲の電界ではなく、空間上のある一点の電界を扱うイメージ。
数学におけるガウスの定理は、またの名をベクトルの発散という。
\[\int \boldsymbol{E・n}dS=\int {\mathrm{div}\boldsymbol{E}}dV\] という式で表される。右辺に含まれる\(\mathrm{div}\boldsymbol{E}\)というのは単位体積当たりから湧き出してくる電場の大きさ(発散)を表している。 各方向の変化を足したものと考えてよい。
\[\mathrm{div}\boldsymbol{E}=\nabla・\boldsymbol{E}=\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\] と定義できる。
下図に示すように、Pを一つの頂点として、各座標軸にそって立方体を考えよう。この六つの面を通って出ていく電気力線の総本数が直方体の内部の電荷と関係付けられている。 まずx軸に垂直な二つの面、図では右と左の面、を考える。外向きの法線方向は、右側ではx、左面では-x方向である。面内での\(E_x\)の変化を無視すれば、積分のこの部分は、
\[E_x(x + \Delta x,y,z)\Delta y\Delta z-E_x(x ,y,z)\Delta y\Delta z\] \[\simeq \frac{ \partial E_x }{ \partial x }\Delta x\Delta y\Delta z\] と近似できる。同様にy軸、z軸に垂直な2くみの面の寄与を求めこれらを足して電気力線の合計を出すと
\[\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\Delta x\Delta y\Delta z\]
一方、直方体の中にある電荷は、体積密度を\(\rho\)とすれば\(\rho\Delta x\Delta y\Delta z\)と近似できる。これらを先の積分式に入れると、ガウスの法則は、
\[\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }\Delta x\Delta y\Delta z=\frac{\rho}{\epsilon_0}\Delta x\Delta y\Delta z\] と書くことが出来る。
この式から\(\Delta x\Delta y\Delta z\)を消去し、ナブラで表現すれば
\[\mathrm{div}\boldsymbol{E}=\nabla・\boldsymbol{E}=\frac{ \partial E_x }{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z }=\frac{\rho}{\epsilon_0}\]
と表すことが出来る。

電気力線と電束
磁束線
ホームに戻る