磁界と電流には相互的な関係がある。
いま、無限長の導線に電流\(I\)が流れている。


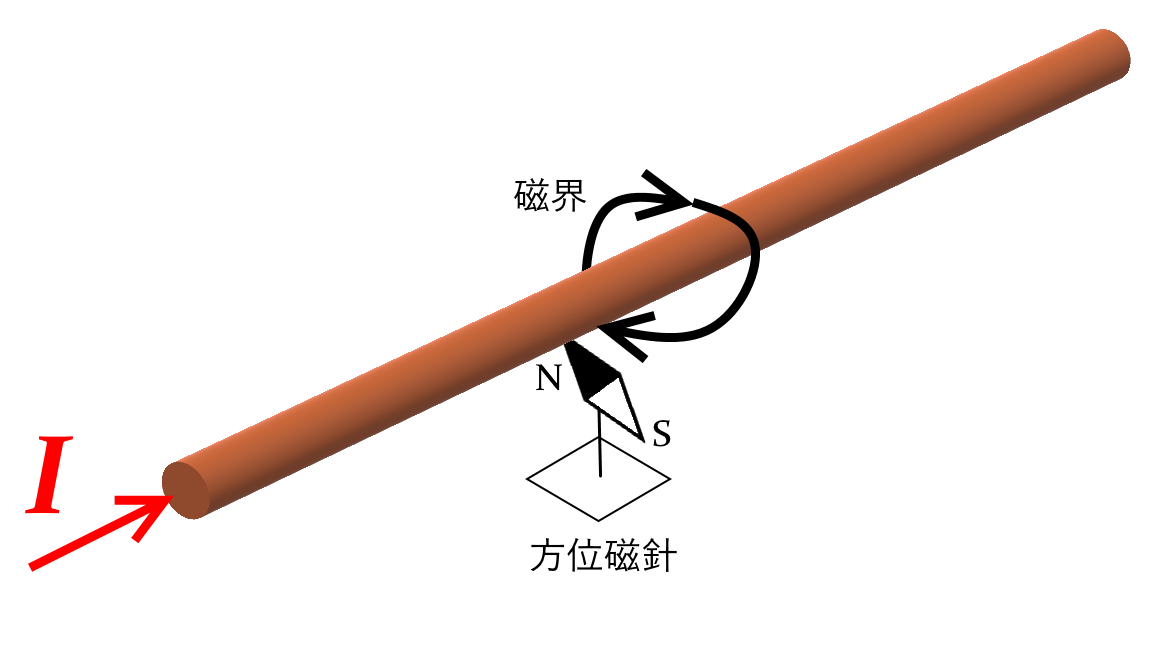
この時、磁界は電流に対して右ねじを回す向きに現れる。
これを右ねじの法則といい、これによる作用する力\(F\)は、
\[F=I×B\] \[F=\frac{μ_0I_1I_2}{2\pi r}\] となる。この式の\(B\)は磁界の大きさを表す量、すなわち磁束の密度を示すことから磁束密度という。
磁束密度は、電流が大きいほど高く、導体から離れるほど低くなる。真空中での磁束密度は
力と磁束密度は \[F=I_1B\] である。この式から磁束密度の式は \[B= \frac{μ_0}{4\pi} \frac{I_2}{r^2} l\sin\theta\] となる。
この時、\(μ_0\)は真空の透磁率といい、
\[μ_0=4\pi×10^{-7}\] と表せる。
ここで、電束密度と磁界の強さは別のものである。
電束密度\(B\)に対し、電界の強さは\(H\)と表記しこれらは
\[B=μ_0H\] という関係がある。
電流による電界に対応する、磁束密度によって作られる線を磁束線という。
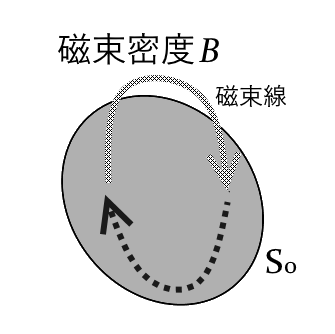
またこの磁束線は、閉曲線であり、任意の閉曲面\(S_0\)を定義した時、入ってくる磁束の量と出て行く磁束の量は同じである。
更に、磁界においてもガウスの法則が成り立つ。
上記のように任意の閉曲面\(S_0\)を考えた時、 \[\int_SB_n=0\]\[\mathrm{div}B=\nabla・B=0\] となる。これらの式は、磁束は発散がない、すなわち入る量と出る量が同じであることを示している。
電界におけるガウスの法則の積分系と同様に閉曲面\(S_0\)を貫く磁束\(Φ_B\)は \[Φ_B=\int_S \boldsymbol{B・n}dS=\int_SB_ndS=\int_SBS\cos\theta\] となる。
この式自体も閉曲面\(S_0\)を通過する電束の式とほぼ同じ形になっている。
このように磁界と電界は非常に似た性質を持っている。


さて、電流から磁界が発生することを含めて説明してきた。次は具体的に電流と磁界の関係について説明していこう。

---

～磁界と電流～
電流と磁界の関係
Chapter2～磁力線と磁束～

関連法則
ガウスの法則


ホームに戻る