ベクトル
Chapter1 ~ベクトルの定義と基本~
それでは早速、ベクトルの定義をしていく。
まず、ある空間を考える(ここでは簡単のため2次元空間を用いる)。
この空間内に点P、点Qを置き点PからQに向けて矢印でつなぐ。
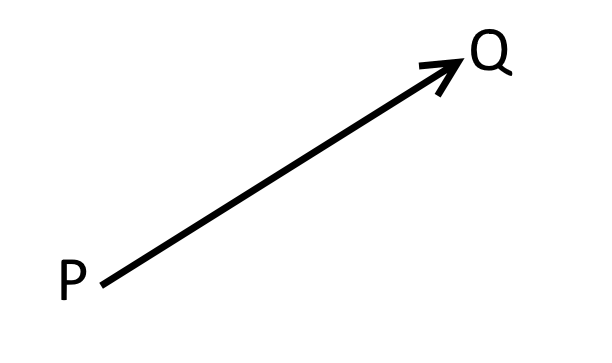
つないだ図がこれ。
このように始点と終点を矢印で結んだものを有効成分という(この場合の始点は点P、終点は点Qとしている)。
この有効成分は方向、量、置かれる場所の3つから成り立つ。
この中で置かれている場所を除く方向、量の2つのみに注目したものをベクトルという。
少し回りくどい言い方をしているが、ベクトルが方向、量の2つから成り立つことを定義した。
このベクトルを文字で書き表すと、\(\overrightarrow{PQ}\)または、PQとなる。
等しいベクトル
置かれている場所を考えない、すなわち
置かれている場所は違っても同じ方向、同じ量であれば等しいベクトルとして扱える。
逆に言えば方向が同じで量が異なる、あるいは量が同じで方向が異なる場合は別の値という扱いになる。
更に噛み砕いて説明するとベクトルを平行移動させただけであれば同じベクトルとして扱って良いのである。
ただし、これはあくまでベクトルの場合であって先に説明した有効成分では別のものである。
ベクトルの和と差
まとめると、ベクトルの和は、「2つの移動量の合計」と考えることができる。
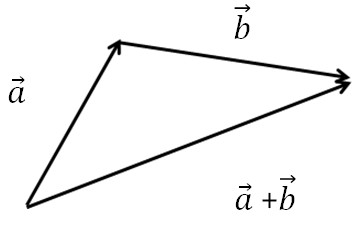
これがベクトルの和である。
次にベクトルの差は、「逆ベクトルとの和」と考える。
\(\overrightarrow{b}\)の逆ベクトル(方向が逆)のベクトル、すなわち-\(\overrightarrow{b}\)を考えた時下図のようになる。
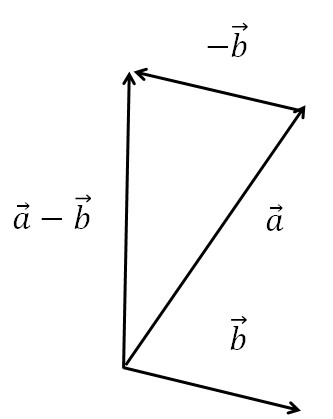
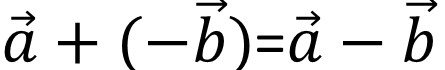
これがベクトルの差である。
ここまで、ベクトルの考え方を始めとして基本となる和と差まで説明した。
ベクトルは大きさと方向を定義するが、一般に大きさのみを表す量も存在しそれをスカラー量という。
では次の章ではベクトル量とスカラー量の違いについて説明しよう。
まず、ある空間を考える(ここでは簡単のため2次元空間を用いる)。
この空間内に点P、点Qを置き点PからQに向けて矢印でつなぐ。

つないだ図がこれ。
このように始点と終点を矢印で結んだものを有効成分という(この場合の始点は点P、終点は点Qとしている)。
この有効成分は方向、量、置かれる場所の3つから成り立つ。
この中で置かれている場所を除く方向、量の2つのみに注目したものをベクトルという。
少し回りくどい言い方をしているが、ベクトルが方向、量の2つから成り立つことを定義した。
このベクトルを文字で書き表すと、\(\overrightarrow{PQ}\)または、PQとなる。
更に噛み砕いて説明するとベクトルを平行移動させただけであれば同じベクトルとして扱って良いのである。
ただし、これはあくまでベクトルの場合であって先に説明した有効成分では別のものである。
まとめると、ベクトルの和は、「2つの移動量の合計」と考えることができる。
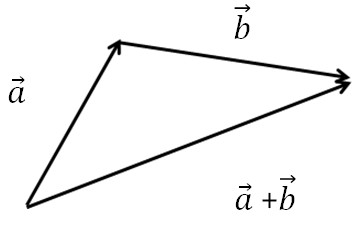
これがベクトルの和である。
次にベクトルの差は、「逆ベクトルとの和」と考える。
\(\overrightarrow{b}\)の逆ベクトル(方向が逆)のベクトル、すなわち-\(\overrightarrow{b}\)を考えた時下図のようになる。

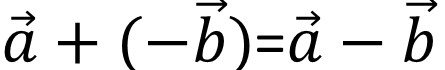
これがベクトルの差である。
ここまで、ベクトルの考え方を始めとして基本となる和と差まで説明した。
ベクトルは大きさと方向を定義するが、一般に大きさのみを表す量も存在しそれをスカラー量という。
では次の章ではベクトル量とスカラー量の違いについて説明しよう。