ベクトル

これまで、ベクトルの基本的な定義などを説明してきた。
次のステップとしてベクトルの勾配、発散、回転について説明を行う。


ベクトルの回転(rotation)

次にベクトルの回転について説明する。

回転(rotation)とはまさにその名の通り回転を示す。

ベクトルの回転とは、あるベクトルが左右どちらにどのくらい回転しているのか、あるいは回転していないのかを表すのに使用される。

3次元(立体)空間を通過するベクトル場Aを考える。
このベクトルを座標平面ごとにAx,Ay,Azと分けて考えてみる。
これを式で表すと
\[\mathrm{rot}\boldsymbol{A} =\nabla×\boldsymbol{A}\] \[= (\frac{ \partial A_z}{ \partial y }-\frac{ \partial A_y}{ \partial z })\boldsymbol{i}\] \[+(\frac{ \partial A_x }{ \partial z }-\frac{ \partial A_z }{ \partial x })\boldsymbol{j}\] \[+(\frac{ \partial A_y }{ \partial x }-\frac{ \partial A_x }{ \partial y })\boldsymbol{k}\] となる。ここで\(\nabla\)(ナブラ)とAは外積の関係となるので注意。
ベクトルの回転はベクトルである。これは下図のようにｘ軸、ｙ軸、ｚ軸に平行な軸のまわりを回っている循環量密度を第１項、第２項、第３項に持つようなベクトルを考える。


といってもイメージがつきにくいであろう。
ここでAxAyAzをそれぞれ風と考え、回転方向を表すベクトルを風によって回転する風車と考え下図のようにする。
この風車はｘ軸の周りを回転している。Ａは流速を表し、ｄを風車の直径とし、流速のｚおよびｙ成分(ｙ-ｚ面内)を考える。
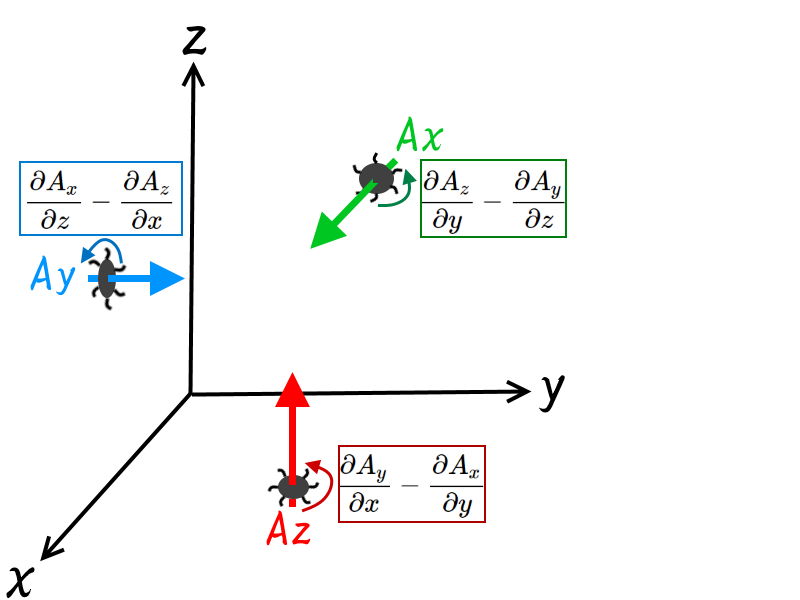
ｘ軸での回転スピードは、 　\[\frac{A_z(y+d)-A_z(y)}{ d }\rightarrow\frac{\partial A_z}{\partial y}\] 　\[\frac{A_y(z+d)-A_y(z)}{ d }\rightarrow\frac{\partial A_y}{\partial z}\] 　従って、ｘ軸のまわりの回転速度は、
\[\frac{\partial A_z}{\partial y}-\frac{\partial A_y}{\partial z}\] 符号は右ネジの法則に従って定義する。
同様に考えて、ｙ軸、ｚ軸のまわりの回転速度は、
\[\frac{\partial A_x}{\partial z}-\frac{\partial A_z}{\partial x}\] \[\frac{\partial A_y}{\partial x}-\frac{\partial A_x}{\partial y}\] となる。

ｘ、ｙ、ｚ軸方向の単位ベクトル\(\boldsymbol i\)、\(\boldsymbol j\)、\(\boldsymbol k\)を用いて、風車の回転速度は \[rot\boldsymbol{A} =\nabla×\boldsymbol{A}\] \[= (\frac{ \partial A_z}{ \partial y }-\frac{ \partial A_y}{ \partial z })\boldsymbol{i}\] \[+(\frac{ \partial A_x }{ \partial z }-\frac{ \partial A_z }{ \partial x })\boldsymbol{j}\] \[+(\frac{ \partial A_y }{ \partial x }-\frac{ \partial A_x }{ \partial y })\boldsymbol{k}\] となる。\(\nabla×\boldsymbol{A}\)は\(\mathrm{rot}\boldsymbol{A}\)または\(\mathrm{curl}\boldsymbol{A}\)と書くことが出来る。
直線状導体に流れる電流から発生する磁界の関係はまさにこのベクトルの回転の関係になっている。

磁界は電流のベクトルの回転ベクトルとして現れる。

---

～勾配、発散、回転～

Chapter3-2～ベクトルの発散～




項目一覧に戻る