ベクトル

これまで、ベクトルの基本的な定義などを説明してきた。
次のステップとしてベクトルの勾配、発散、回転について説明を行う。


ベクトルの発散(divergence)

それでは次にベクトルの発散について説明する。

発散（divergence）とはその名の通り湧き出しを示す。


では早速ベクトルの発散に関して説明を行っていく。
3次元空間のある領域にベクトル場Eを考える。
この時、ベクトル解析におけるスカラー場の発散をdiv\(E\)と表す。
これを式で表すと
\[\mathrm{div}\boldsymbol{E} = \frac{ \partial E_x}{ \partial x }\frac{ \partial E_y }{ \partial y }\frac{ \partial E_z }{ \partial z }\] \[= \frac{ \partial}{ \partial x}+\frac{ \partial}{ \partial y}+\frac{ \partial}{ \partial z}(E_{xi}+E_{yj}+E_{zk})\] となる。この式の左辺はベクトル関数を示し、右辺はスカラーの座標を示す。つまりベクトルの発散とはベクトル関数からからスカラーを作っていることを示している。

最初に発散を湧き出しとした。今度はなぜそう言えるかを示す。
微小体積からのベクトルの湧き出し\(\mathrm{div}\boldsymbol{E}dV\)を考える。
図のような微小体積、各辺が\(dx,dy,dz\)の直方体を考える。つまり体積は\(dV=dxdydz\)である。これを先に説明した式に代入すると
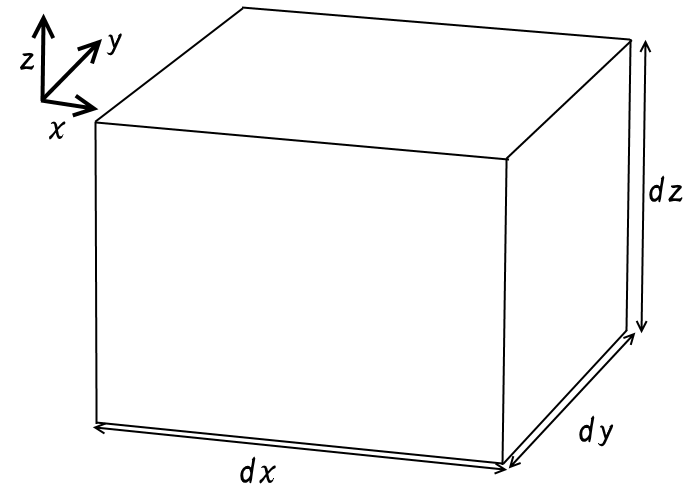
\[\mathrm{div}\boldsymbol{E}dV= (\frac{ \partial E_x}{ \partial x }+\frac{ \partial E_y }{ \partial y }+\frac{ \partial E_z }{ \partial z })dxdydz\] \[\frac{ \partial E_x}{ \partial x }dxdydz+\frac{ \partial E_y }{ \partial y }dxdydz+\frac{ \partial E_z }{ \partial z }dxdydz\] まず右辺の最初の項を見ると\(\frac{ \partial E_x}{ \partial x }\)である。これはEのｘ成分に対するx方向の変化率について書いてある。
このdxをかけた量はx方向にdxだけ移動する間のベクトルの増加量である。
ここで、\(\frac{ \partial E_x}{ \partial x }\)にはさらにdydzがかけられている。dydzはこれは直方体のyz面の面積に相当する。
つまり１項は直方体のx方向に向かってyz面を通り抜けるベクトルがどれだけ増加したかを表す。下図はそのイメージである。
your browser does not support HTML5 Canvas.
同様に2項目3項目はそれぞれ、\(\frac{ \partial E_y}{ \partial y }\)は、xz平面をy方向に向かって通り抜けるベクトルがどのくらい増加するか、\(\frac{ \partial E_z}{ \partial z }\)は、xy平面をz方向に向かって通り抜けるベクトルがどのくらい増加するかを示す。
このようにdivEは単位体積あたりのベクトルの増加量を示す。

この単位面積あたりに対してベクトルが増加する様子が、水やガスと言った流体が湧き出る様子に似ていることからよく湧き出るという説明がされる。

また最初に紹介した式は \[\mathrm{div}\boldsymbol{E} = \frac{ \partial E_x}{ \partial x }\frac{ \partial E_y }{ \partial y }\frac{ \partial E_z }{ \partial z }\] \[=\nabla・\boldsymbol{E}\] と表すことができる。この時逆さ三角のような記号\(\nabla\)をベクトル演算子ナブラという。