ベクトル

これまで、ベクトルの基本的な定義などを説明してきた。
次のステップとしてベクトルの勾配、発散、回転について説明を行う。


3-1ベクトルの勾配(gradient)

それではまずベクトルの勾配から説明する。

勾配(gradient)とはその名の通り斜面を示す。


ではベクトル解析におけるスカラー場の勾配（gradient）について説明する。まずこの式を見てほしい。
\[\mathrm{grad}f = \frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}\] この時\(f\)はスカラー関数という。
関数とはaを決めればbが決まるという数値のことであり、この場合スカラーすなわちある量が決まれば勾配grad\(f\)が決まるということを表す。
この式はスカラー関数\(f\)から三次元ベクトルを一つ作っている。
この式の右辺は3次元の各座標に対応しており、 \(x\)の変化率に対する\(f\)の変化率、\(y\)の変化率に対する\(f\)の変化率、\(z\)の変化率に対する\(f\)の変化率を示す。
勾配とはこれらの変化率の値を大きさにもつベクトルに対応させたベクトル場である。

ここで説明の簡単のため二次元で考えると \[\mathrm{grad}f = \frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\] 　となる。これを具体的に数値を入れて考えてみると
\[f = 2x + 3y\] となり \[\frac{\partial f}{\partial x}=2　　　　　\frac{\partial f}{\partial y}=3\]
すなわち勾配の座標は \[\mathrm{grad}f = (2 , 3)\] となる。 これを同様に三次元で考えると
\[f=2x+3y+5z\]
という式があったとしよう。この式の場合
\(x\)の変化率に対する\(f\)の変化率=2
\(y\)の変化率に対する\(f\)の変化率=3
\(z\)の変化率に対する\(f\)の変化率=5
となる。したがって
\[\mathrm{grad}f = (2 , 3 , 5)\]となる。ではいったいこのｆは何を表しているか。次のグラフを見てほしい。
　ここではわかりやすくするため二次元で考えている。x方向とy方向の変化率をそれぞれx方向とy方向の成分としたベクトル\[\mathrm{grad}f = \frac{\partial f}{\partial x},\frac{\partial f}{\partial y}\]を考えればまとめて表記できる。
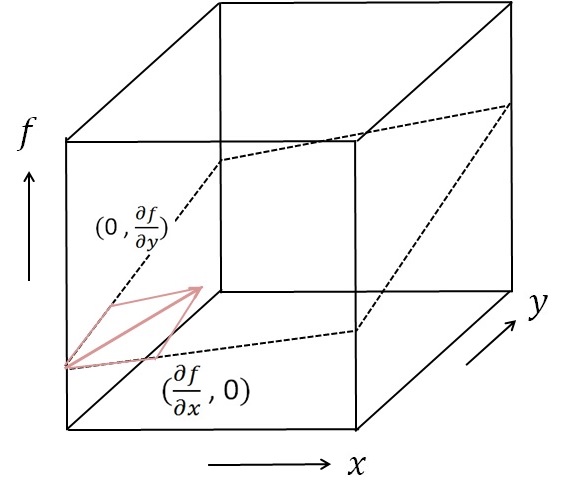
したがって\(\mathrm{grad}\)はｘ方向の変化率とｙ方向の変化率を合成した一番変化率の高い方向を向いているベクトルとなる。gradientが勾配だというのがわかっていただけただろうか。